- Detalles
- Escrito por Bernardo Zagalaz Lijarcio
Tubos sonoros
Se llaman tubos sonoros aquellos que contienen una columna gaseosa (columna de aire) capaz de producir sonido al ser convenientemente excitada. El cuerpo sonoro es la columna gaseosa, y no el tubo que la contiene; en efecto, éste tiene la importante función de definir la forma de aquella pero fuera de esto, influye relativamente poco sobre los fenómenos sonoros. Los tubos sonoros pueden ser cerrados, es decir, que poseen una sola abertura y tubos abiertos, que poseen dos o más.Vibración de la columna de aire contenida en un tubo
Las columnas de aire contenidas en los tubos sonoros se comportan, desde ciertos puntos de vista, como cuerdas musicales, por lo tanto las columnas de aire vibrantes poseen nodos, o sea puntos donde la vibración es nula, y vientres, equidistantes de los anteriores, donde la vibración alcanza su máxima amplitud.La vibración de las columnas de aire es longitudinal; los nodos serán por tanto, puntos de condensación y los vientres puntos de dilatación o rarefacción; en los extremos cerrados siempre se producen nodos y en los extremos abiertos generalmente se producen vientres. El punto de excitación no puede ser un nodo, pero no necesita ser un vientre, pudiendo estar en un punto intermedio. No es necesario que las aberturas de un tubo coincidan con los extremos, pudiendo éstos estar cerrados y haber una o más aberturas en otras partes del tubo (la gaita).
Una columna de aire puede vibrar con toda su longitud o dividida en segmentos iguales lo mismo que las cuerdas; en el primer caso se obtiene el sonido llamado fundamental, y en los otros los armónicos: segundo, si la columna vibra dividida en mitades; tercero, si vibra en tercios, etc.
Tomando como punto de partida el que en los extremos de un tubo abierto, sólo pueden haber vientres de vibración, el tubo producirá su fundamental cuando vibre con un nodo único en su centro. Cuando el tubo produce su segundo armónico, producirá dos nodos y tres vientres; cuando produce su tercer amónico, producirá tres nodos y 4 vientres, y así sucesivamente.
En los Tubos Cerrados, la onda se forma con un nodo en el extremo cerrado y un vientre en el extremo abierto.
A igualdad de longitud de tubo, el tubo abierto produce un sonido de frecuencia doble que el cerrado. Los tubos abiertos emiten la serie completa de armónicos correspondientes a su longitud, mientras que los cerrados, emiten sólo los armónicos de orden impar. Como tubo cerrado está la Flauta Travesera y como tubos abiertos todos los demás: Clarinetes*, Oboes, Fagotes, Saxofones, Trompetas, Trompas, etc.
Clasificación de los tubos sonoros
Los tubos sonoros se pueden clasificar de las siguientes formas:- Según el modo de excitación de la columna de aire
- Según la obtención de la escala
- Según su forma interior
Tubos de embocadura son tubos sonoros que poseen una abertura convenientemente dispuesta llamada embocadura, uno de cuyos bordes es biselado. Contra este borde incide una corriente de aire que se divide en dos ramas; la rama que penetra en el tubo origina pequeñas vibraciones que a su vez excitan por resonancia la columna aérea contenida en el tubo. Estos se pueden dividir en:
- Tubos de embocadura directa. Los tubos de embocadura directa son aquellos en que la corriente de aire es dirigida sobre la embocadura directamente por los labios del ejecutante. La siguiente figura muestra una embocadura de flauta travesera que es el prototipo de los instrumentos de embocadura directa.
- Tubos de embocadura indirecta son aquellos donde la corriente de aire, producida mecánicamente o por el ejecutante, pasa por un tubo llamado portaviento antes de incidir sobre el bisel de la embocadura. Las siguientes figuras representa la parte superior de una flauta de pico y a un tubo de órgano, el órgano tiene varias clases de tubos, siendo uno de ellos “tubos de bisel”.
Tubos de lengüeta están formados por pequeñas laminillas elásticas, generalmente de metal o de madera (caña) que sujetas a un soporte de manera conveniente, vibran al paso de una corriente aérea, produciendo sonido; se las clasifica según su mayor o menor libertad de movimiento en dos tipos diferentes: libres y batientes.
- Tubos de lengüetas libres aquellas que vibran libremente a uno y otro lado del plano que determinan cuando están en reposo; esto se obtiene con un soporte cuyos únicos puntos de contacto con la lengüeta son aquellos en que ésta se halla fijada a aquel. Las lengüetas libres son siempre de metal; se utilizan en el armonio, el acordeón, la armónica y otros aerófonos libres.
- Tubos de lengüetas batientes aquellas que baten contra el soporte al cual están sujetas. En estas las vibraciones se hallan restringidas por la presencia del soporte, cosa que no ocurre con las lengüetas libres.
Las lengüetas batientes se dividen a su vez en simples y dobles, según el tipo de soporte que utilizan.- Tubos de lengüetas batientes simples, llamadas corrientemente lengüetas simples (cañas), son aquellas que se colocan sobre los bordes de una abertura contra los cuales baten.
Son utilizadas por los clarinetes, saxofones y por los juegos de lengüeta del órgano, siendo de metal en este instrumento y de madera (caña) en los primeros.
- Tubos de lengüetas batientes dobles, llamadas corrientemente lengüetas dobles, son aquellas que utilizan como soporte otra lengüeta contra la cual baten, batiendo ésta a su vez contra la primera.
Las lengüetas batientes dobles se construyen siempre de madera (caña) siendo utilizadas por los oboes y fagotes. También utilizan lengüetas dobles algunos instrumentos como la gaita (la gaita presenta la particularidad de utilizar simultáneamente lengüetas simples y dobles).
- Tubos de lengüetas batientes simples, llamadas corrientemente lengüetas simples (cañas), son aquellas que se colocan sobre los bordes de una abertura contra los cuales baten.
- Tubos de lengüeta labial o membranácea. Los principales son trompas, trompetas, trombones y tuba, en este tipo de instrumentos los labios del ejecutante actúan del mismo modo que una lengüeta batiente doble, por lo cual se dice que forman una lengüeta doble membranácea.
En estos instrumentos la boquilla es muy diferente a la los instrumentos de lengüeta y de embocadura, pues se la construye con el objeto de ser adosada a los labios del ejecutante en lugar de ser introducida entre ellos.
Los procedimientos seguidos para obtener columnas aéreas de diferente longitud sobre un mismo tubo sonoro pueden reducirse a dos:
Perforar sobre sus paredes orificios de tamaño y posición convenientes que permitan variar la longitud acústica del tubo, determinando la longitud de la columna aérea en el momento en que se destapa o cierra un orificio dado. (Tubos con orificios: instrumentos de viento madera, etc.)
Estos orificios se controlan mediante los dedos o mediante llaves; éstas son palancas o sistemas de palancas que permiten controlar aquellos orificios cuyo diámetro excede al ancho de la yema de los dedos o cuya situación sobre el tubo no permite un control directo. La siguiente figura representa una llave cualquiera; la almohadilla destinada a cubrir el orificio controlado por la llave, que se halla sobre la cara interna de ésta, se llama “zapatilla”.
No es indiferente el diámetro de los orificios que se perforan sobre un tubo sonoro; para una misma longitud acústica, un orificio de diámetro grande producirá un sonido de frecuencia algo mayor (más agudo) que uno de diámetro más pequeño.
En ciertos instrumentos como el fagot, los orificios exteriores no indican la posición real del orificio sobre la pared interna del instrumento, pues se perforan oblicuamente para agruparlos mejor bajo el control de la mano.
Los instrumentos que utilizan este sistema de orificios forman su escala variando la longitud acústica de sus tubos; cada columna aérea produce su fundamental y un corto número de parciales que se obtienen variando la fuerza del soplo y la tensión de los labios; en los tubos de lengüeta, la obtención de parciales se facilita mediante un portavoz (llaves de octava), pequeño orificio situado cerca del extremo superior de estos tubos, que actúa sobre las columnas de aire como un dedo apoyado ligeramente sobre una cuerda vibrante, es decir, favoreciendo la producción de los parciales de dichas columnas. Algunos instrumentos utilizan dos portavoces (saxofón).
Variar su longitud real mediante porciones de tubo que se conectan al tubo principal obteniéndose así las columnas aéreas deseadas (Tubos de longitud variable: instrumentos de viento metal, etc.). Se utilizan tres procedimientos:
- La Vara (Trombón de varas): Consiste en cortar el tubo del instrumento y adaptar a sus extremos un tubo en forma de “U”, cuyas ramas enchufan telescópicamente sobre las ramas del tubo fijo. Mediante la vara, la longitud del tubo puede ser variada continuamente, permitiendo obtener diferentes sonidos.
- Los Pistones (Trompetas, Trombón de pistones, etc.): Generalmente cuando la longitud es variada mediante pistones, uno de éstos, que se considera el primero, produce una serie de parciales situados un tono más bajo que la serie original; otro, considerado segundo, produce un descenso de un semitono y un tercero, produce un descenso de tono y medio. Los pistones pueden utilizarse simultáneamente para lograr descensos mayores. Algunos instrumentos poseen pistones que provocan descensos mayores de un tono y medio (cuarto y quinto pistón)
- Las Válvulas Rotatorias (Trompas, Tubas, etc.): Todo lo que he dicho respecto de los pistones puede aplicarse igualmente a las válvulas rotatorias
Los tubos prismáticos se utilizan solamente en ciertos registros de órgano y en algunos instrumentos primitivos, los demás instrumentos poseen tubos cilíndricos (flauta travesera,....) cónicos (saxofón, fagot.....) o de tipos intermedios (clarinete, oboe, trompeta.....).
| CLASIFICACIÓN DE LOS TUBOS SONOROS | ||||
|---|---|---|---|---|
| Según el Modo de Excitación de la Columna de Aire | Tubos de Embocadura | Directa | Flta. Travesera,… | |
| Indirecta | Flta. de pico, Tubos órgano,… | |||
| Tubos de Lengüeta | Libres | Arcordeón, Armónica,… | ||
| Batientes | Simples | Clte., Sax., Tubos órgano… | ||
| Dobles | Oboe, Fagot,… | |||
| Tubos de lengüeta labial o membranácea | Trompeta, Trompa, trombón, Tuba… | |||
| Según la obtención de la escala | Tubos con orificios | Instrumentos de Viento Madera,… | ||
| Tubos de longitud variable | Vara | Trombón de varas | ||
| Pistones | Trompeta,… | |||
| Válvulas Rotatorias | Trompa, Tuba,… | |||
| Según su Forma Interior | Cónicos | Saxofón, Fagot,… | ||
| Cilíndricos | Flauta travesera, Clarinete,… | |||
| Prismáticos | Instr. Primitivos, algunos tubos del órgano… | |||
Bibliografia
- Acústica físico-musical de Antonio Clavo-Manzano (Ed. Real Musical)
- Acústica Musical y Organología de Tirso de Olazábal (Ed. Ricordi)
Ondas estacionarias en tubos abiertos o cerrados
Movimiento ondulatorio
Acústica
Ondas estacionarias
en tubosVelocidad del sonido en una barra
Velocidad del sonido en un gas
El resonador de Helmholtz
Análisis de Fourier
Efecto Doppler(I)Efecto Doppler (II)Efecto Doppler (III)Tubos abiertosTubos cerrados
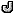Actividades
Ya hemos visto en este capítulo como son las ondas estacionarias en una cuerda. Ahora veremos las ondas estacionarias que se producen en los tubos abiertos o cerrados por un extremo.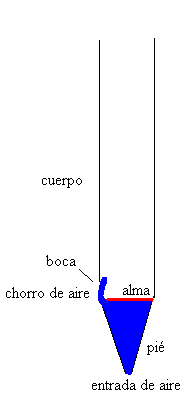
Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido.
Las versiones modernas de estos instrumentos de viento son las flautas, las trompetas y los clarinetes, todos ellos desarrollados de forma que el intérprete produzca muchas notas dentro de una amplia gama de frecuencias acústicas.
El órgano es un instrumento formado por muchos tubos en los que cada tubo da una sola nota. El órgano de la sala de conciertos de La Sydney Opera House terminado en 1979 tiene 10500 tubos controlados por la acción mecánica de 5 teclados y un pedalero.
El tubo de órgano es excitado por el aire que entra por el extremo inferior. El aire se transforma en un chorro en la hendidura entre el alma (una placa transversal al tubo) y el labio inferior. El chorro de aire interacciona con la columna de aire contenida en el tubo. Las ondas que se propagan a lo largo de la corriente turbulenta mantienen una oscilación uniforme en la columna de aire haciendo que el tubo suene.
Tubos abiertos
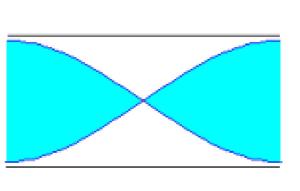
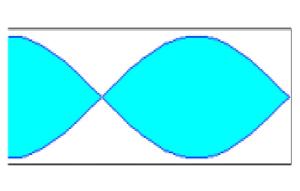
Si un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración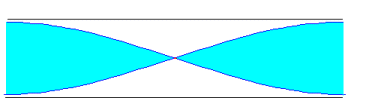
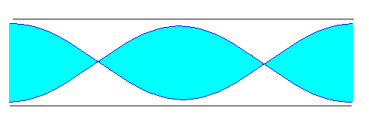
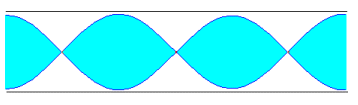
Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que
L=l /2, L=l , L=3l /2, ... en general L=nl /2, n=1, 2, 3... es un número entero
Considerando que l =vs/f (velocidad del sonido dividido la frecuencia)
Las frecuencias de los distintos modos de vibración responden a la fórmula
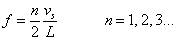
Tubos cerrados
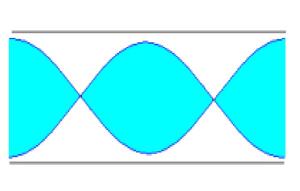
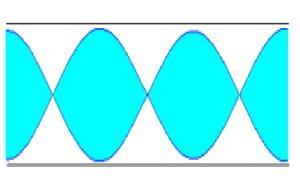
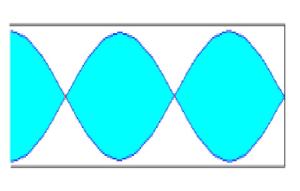
Si el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es l /4. La longitud L del tubo es en las figuras representadas es L=l /4, L=3l /4, L=5l /4...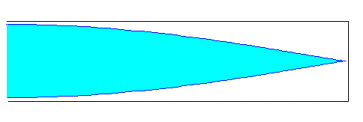
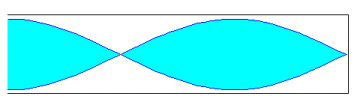
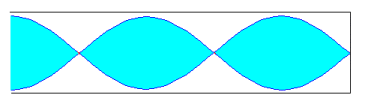
En general L=(2n+1) l /4; con n=0, 1, 2, 3, ...
Las frecuencias de los distintos modos de vibración responden a la fórmula
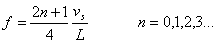
Leyes de Bernoulli
Las fórmulas obtenidas explican las denominadas leyes de Bernoulli:
La frecuencia del sonido en un tubo es:
- Directamente proporcional a la velocidad del sonido vs en el gas que contiene el tubo
- Inversamente proporcional a la longitud del tubo L
- En un tubo abierto, se puede producir el sonido que corresponde a la frecuencia fundamental (n=1) y sus armónicos (n=2, 3, 4, ..)
- En un tubo cerrado, se puede producir el sonido que corresponde a la frecuencia fundamental y los armónicos impares (2n+1=3, 5, 7, ...).
- En dos tubos idénticos y con el mismo gas, uno abierto y otro cerrado, el abierto produce un sonido cuya frecuencia (fundamental) es el doble que la del cerrado.
Actividades
Tubo abierto por ambos extremos:
Se activa la casilla titulada Abierto por ambos extremos.
Comprobar que si la longitud del tubo L=1 m, y la velocidad del sonido vs =340 m/s la frecuencia del modo fundamental es f0=170 Hz.
Se pulsa el botón titulado Siguiente, comprobar que las frecuencias de los armónicos son múltiplos de la frecuencia fundamental: 340 Hz, 510 Hz, etc.
Tubo abierto por un extremo
Se activa la casilla titulada Abierto por un extremos.
Comprobar que si la longitud del tubo L=1 m, y la velocidad del sonido vs =340 m/s la frecuencia del modo fundamental es f0=85 Hz (la mitad que en el tubo abierto)
Se pulsa el botón titulado Siguiente, comprobar que las frecuencias de los armónicos son múltiplos im
ONDAS ESTACIONARIA EN TUBOS ABIERTOS Y CERRADO
Ya hemos visto en este capítulo como son las ondas estacionarias en una cuerda. Ahora veremos las ondas estacionarias que se producen en los tubos abiertos o cerrados por un extremo.Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido.Las versiones modernas de estos instrumentos de viento son las flautas, las trompetas y los clarinetes, todos ellos desarrollados de forma que el intérprete produzca muchas notas dentro de una amplia gama de frecuencias acústicas.El órgano es un instrumento formado por muchos tubos en los que cada tubo da una sola nota. El órgano de la sala de conciertos de La Sydney Opera House terminado en 1979 tiene 10500 tubos controlados por la acción mecánica de 5 teclados y un pedalero.El tubo de órgano es excitado por el aire que entra por el extremo inferior. El aire se transforma en un chorro en la hendidura entre el alma (una placa transversal al tubo) y el labio inferior. El chorro de aire interacciona con la columna de aire contenida en el tubo. Las ondas que se propagan a lo largo de la corriente turbulenta mantienen una oscilación uniforme en la columna de aire haciendo que el tubo suene.
Tubos abiertos
Tubo abierto por los dos etremos
Tubo abierto por los dos extremos segunda forma de vibraciónSi un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración
Tubo abierto por los dos extremos tercera forma de vibración
Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que
L=λ /2, L=λ , L=3λ /2, … en general L=nλ/2, n=1, 2, 3… es un número entero
Considerando que λ =vs/f (velocidad del sonido dividido la frecuencia)
Las frecuencias de los distintos modos de vibración responden a la fórmula
Tubos cerrados
Tubo cerrado por un extrmo, primera forma de vibración
Tubo cerrado por un extremo, segunda forma de vibraciónSi el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es λ/4. La longitud L del tubo es en las figuras representadas es L=λ /4, L=3λ/4, L=5λ /4…
Tubo cerrado por un extremo, tercera forma de ibración
En general L=(2n+1)λ/4; con n=0, 1, 2, 3, …
Las frecuencias de los distintos modos de vibración responden a la fórmula
Efecto Doppler acústico
Cuando la fuente de ondas y el observador están en movimiento relativo con respecto al medio material en el cual la onda se propaga, la frecuencia de las ondas observadas es diferente de la frecuencia de las ondas emitidas por la fuente. Este fenómeno recibe el nombre de efecto Doppler en honor a su descubridor.
En primer lugar, vamos a observar el fenómeno, y después obtendremos la fórmula que relaciona la frecuencia de las ondas observadas con la frecuencia de las ondas emitidas, la velocidad de propagación de las ondas vs, la velocidad del emisor vE y la velocidad del observador vO.
Consideraremos que el emisor produce ondas de forma continua, pero solamente representaremos los sucesivos frentes de ondas, circunferencias centradas en el emisor, separados por un periodo, de un modo semejante a lo que se puede observar en la experiencia en el laboratorio con la cubeta de ondas. En la simulación más abajo, fijaremos la velocidad de propagación del sonido en una unidad vs=1, y el periodo de las ondas sea también la unidad, P=1, de modo que los sucesivos frentes de onda se desplazan una unidad de longitud en el tiempo de un periodo, es decir, la longitud de las ondas emitidas es una unidad, l =vsP.
El observador en reposo
Empezamos por el caso más sencillo, en el que el observador está en reposo, a la izquierda o a la derecha del emisor de ondas. Vamos a estudiar diversas situaciones dependiendo de la velocidad del emisor.
Recordaremos que en el estudio de las del movimiento ondulatorio armónico, se estableció la relación entre longitud de onda y periodo, λ=vsP.
El emisor está en reposo (vE=0)
Emisor en reposo ve=vsComo λ =vP, o bien λ =v/f , hay una relación inversa entre longitud de onda l y la frecuencia f.- Observador situado a la derecha del emisor λO<lE
- Observador situado a la izquierda del emisor λO>lE
- Observador situado a la derecha del emisor fO>fE
Si el emisor emite ondas sonoras, el sonido escuchado por el observador situado a la derecha del emisor, será más agudo y el sonido escuchado por el observador situado a la izquierda será más grave. En otras palabras, cuando el emisor se acerca al observador, éste escucha un sonido más agudo, cuando el emisor se aleja del observador, éste escucha un sonido más grave.
Cuando el emisor está en movimiento (vE=vs)
emisor en movimiento ve=vs
cuando la velocidad del emisor vE sea igual que la velocidad de propagación de las ondas en el medio vs (vE=1), la longitud de onda medida por el observador situado a la derecha del emisor es cero. Si el emisor es un avión que va a la velocidad del sonido, los sucesivos frentes de las ondas emitidas se agrupan en la punta o morro del avión.
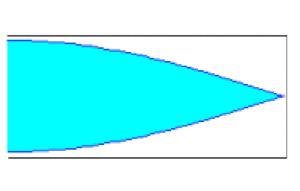
Cuando el emisor está en movimiento (vE>vs)
Cuando la velocidad del emisor vE sea mayor que la velocidad de propagación de las ondas en el medio vs (vE>1), el movimiento ondulatorio resultante es entonces una onda cónica (la envolvente de los sucesivos frentes de onda es un cono con el vértice en el emisor), esta onda se llama onda de Mach u onda de choque, y no es más que el sonido repentino y violento que oímos cuando un avión supersónico pasa cerca de nosotros. Estas ondas se observan también en la estela que dejan los botes que se mueven con mayor velocidad que las ondas superficiales sobre el agua.
La envolvente, es la recta tangente común a todas las circunferencias. En el espacio, los frentes de onda son esferas y la envolvente es una superficie cónica.
Emisor en movimiento ve>vs
Cuando la velocidad del emisor vE sea igual que la velocidad de propagación de las ondas en el medio vs (vE=1), la longitud de onda medida por el observador situado a la derecha del emisor es cero. Si el emisor es un avión que va a la velocidad del sonido, los sucesivos frentes de las ondas emitidas se agrupan en la punta o morro del aviónpares de la frecuencia fundamental: 255 Hz, 425 Hz, etc
ONDAS ESTACIONARIA EN TUBOS ABIERTOS Y CERRADO
Ya hemos visto en este capítulo como son las ondas estacionarias en una cuerda. Ahora veremos las ondas estacionarias que se producen en los tubos abiertos o cerrados por un extremo.Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido.Las versiones modernas de estos instrumentos de viento son las flautas, las trompetas y los clarinetes, todos ellos desarrollados de forma que el intérprete produzca muchas notas dentro de una amplia gama de frecuencias acústicas.El órgano es un instrumento formado por muchos tubos en los que cada tubo da una sola nota. El órgano de la sala de conciertos de La Sydney Opera House terminado en 1979 tiene 10500 tubos controlados por la acción mecánica de 5 teclados y un pedalero.El tubo de órgano es excitado por el aire que entra por el extremo inferior. El aire se transforma en un chorro en la hendidura entre el alma (una placa transversal al tubo) y el labio inferior. El chorro de aire interacciona con la columna de aire contenida en el tubo. Las ondas que se propagan a lo largo de la corriente turbulenta mantienen una oscilación uniforme en la columna de aire haciendo que el tubo suene.
Tubos abiertos
Tubo abierto por los dos etremos
Tubo abierto por los dos extremos segunda forma de vibraciónSi un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración
Tubo abierto por los dos extremos tercera forma de vibración
Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que
L=λ /2, L=λ , L=3λ /2, … en general L=nλ/2, n=1, 2, 3… es un número entero
Considerando que λ =vs/f (velocidad del sonido dividido la frecuencia)
Las frecuencias de los distintos modos de vibración responden a la fórmula
Tubos cerrados
Tubo cerrado por un extrmo, primera forma de vibración
Tubo cerrado por un extremo, segunda forma de vibraciónSi el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es λ/4. La longitud L del tubo es en las figuras representadas es L=λ /4, L=3λ/4, L=5λ /4…
Tubo cerrado por un extremo, tercera forma de ibración
En general L=(2n+1)λ/4; con n=0, 1, 2, 3, …
Las frecuencias de los distintos modos de vibración responden a la fórmula
Efecto Doppler acústico
Cuando la fuente de ondas y el observador están en movimiento relativo con respecto al medio material en el cual la onda se propaga, la frecuencia de las ondas observadas es diferente de la frecuencia de las ondas emitidas por la fuente. Este fenómeno recibe el nombre de efecto Doppler en honor a su descubridor.
En primer lugar, vamos a observar el fenómeno, y después obtendremos la fórmula que relaciona la frecuencia de las ondas observadas con la frecuencia de las ondas emitidas, la velocidad de propagación de las ondas vs, la velocidad del emisor vE y la velocidad del observador vO.
Consideraremos que el emisor produce ondas de forma continua, pero solamente representaremos los sucesivos frentes de ondas, circunferencias centradas en el emisor, separados por un periodo, de un modo semejante a lo que se puede observar en la experiencia en el laboratorio con la cubeta de ondas. En la simulación más abajo, fijaremos la velocidad de propagación del sonido en una unidad vs=1, y el periodo de las ondas sea también la unidad, P=1, de modo que los sucesivos frentes de onda se desplazan una unidad de longitud en el tiempo de un periodo, es decir, la longitud de las ondas emitidas es una unidad, l =vsP.
El observador en reposo
Empezamos por el caso más sencillo, en el que el observador está en reposo, a la izquierda o a la derecha del emisor de ondas. Vamos a estudiar diversas situaciones dependiendo de la velocidad del emisor.
Recordaremos que en el estudio de las del movimiento ondulatorio armónico, se estableció la relación entre longitud de onda y periodo, λ=vsP.
El emisor está en reposo (vE=0)
Emisor en reposo ve=vsComo λ =vP, o bien λ =v/f , hay una relación inversa entre longitud de onda l y la frecuencia f.- Observador situado a la derecha del emisor λO<lE
- Observador situado a la izquierda del emisor λO>lE
- Observador situado a la derecha del emisor fO>fE
Si el emisor emite ondas sonoras, el sonido escuchado por el observador situado a la derecha del emisor, será más agudo y el sonido escuchado por el observador situado a la izquierda será más grave. En otras palabras, cuando el emisor se acerca al observador, éste escucha un sonido más agudo, cuando el emisor se aleja del observador, éste escucha un sonido más grave.
Cuando el emisor está en movimiento (vE=vs)
emisor en movimiento ve=vs
cuando la velocidad del emisor vE sea igual que la velocidad de propagación de las ondas en el medio vs (vE=1), la longitud de onda medida por el observador situado a la derecha del emisor es cero. Si el emisor es un avión que va a la velocidad del sonido, los sucesivos frentes de las ondas emitidas se agrupan en la punta o morro del avión.
Cuando el emisor está en movimiento (vE>vs)
Cuando la velocidad del emisor vE sea mayor que la velocidad de propagación de las ondas en el medio vs (vE>1), el movimiento ondulatorio resultante es entonces una onda cónica (la envolvente de los sucesivos frentes de onda es un cono con el vértice en el emisor), esta onda se llama onda de Mach u onda de choque, y no es más que el sonido repentino y violento que oímos cuando un avión supersónico pasa cerca de nosotros. Estas ondas se observan también en la estela que dejan los botes que se mueven con mayor velocidad que las ondas superficiales sobre el agua.
La envolvente, es la recta tangente común a todas las circunferencias. En el espacio, los frentes de onda son esferas y la envolvente es una superficie cónica.
Emisor en movimiento ve>vs
Cuando la velocidad del emisor vE sea igual que la velocidad de propagación de las ondas en el medio vs (vE=1), la longitud de onda medida por el observador situado a la derecha del emisor es cero. Si el emisor es un avión que va a la velocidad del sonido, los sucesivos frentes de las ondas emitidas se agrupan en la punta o morro del avión
LAS ONDAS Y SUS CARACTERÍSTICAS
 |
| Onda estacionaria (el nodo no vibra) |
Pulso y tren de ondas
Genera ondas o pulsos en una cuerda tensa
Tipos de ondas
Olas en la superficie del mar
Una onda es una perturbación que se propaga desde el punto en que se produjo hacia el medio que rodea ese punto.
Las ondas materiales (todas menos las electromagnéticas) requieren un medio elástico para propagarse.
Las ondas materiales (todas menos las electromagnéticas) requieren un medio elástico para propagarse.
El medio elástico se deforma y se recupera vibrando al paso de la onda.
La perturbación comunica una agitación a la primera partícula del medio en que impacta -este es el foco de las ondas- y en esa partícula se inicia la onda.
La perturbación se transmite en todas las direcciones por las que se extiende el medio que rodea al foco con una velocidad constante en todas las direcciones, siempre que el medio sea isótropo ( de iguales características físico- químicas en todas las direcciones ).
Todas las partículas del medio son alcanzadas con un cierto retraso respecto a la primera y se ponen a vibrar: recuerda la ola de los espectadores en un estadio de fútbol.
La forma de la onda es la foto de la perturbación propagándose, la instantánea que congela las posiciones de todas las partículas en ese instante.
Curiosamente, la representación de las distancias de separación de la posición de equilibrio de las partículas al vibrar frente al tiempo dan una función matemática seno que, una vez representada en el papel, tiene forma de onda.
Podemos predecir la posición que ocuparán dichas partículas más tarde, aplicando esta función matemática.
La perturbación se transmite en todas las direcciones por las que se extiende el medio que rodea al foco con una velocidad constante en todas las direcciones, siempre que el medio sea isótropo ( de iguales características físico- químicas en todas las direcciones ).
Todas las partículas del medio son alcanzadas con un cierto retraso respecto a la primera y se ponen a vibrar: recuerda la ola de los espectadores en un estadio de fútbol.
La forma de la onda es la foto de la perturbación propagándose, la instantánea que congela las posiciones de todas las partículas en ese instante.
Curiosamente, la representación de las distancias de separación de la posición de equilibrio de las partículas al vibrar frente al tiempo dan una función matemática seno que, una vez representada en el papel, tiene forma de onda.
Podemos predecir la posición que ocuparán dichas partículas más tarde, aplicando esta función matemática.
El movimiento de cada partícula respecto a la posición de equilibrio en que estaba antes de llegarle la perturbación es un movimiento vibratorio armónico simple.
Una onda transporta energía y cantidad de movimiento pero no transporta materia: las partículas vibran alrededor de la posición de equilibrio pero no viajan con la perturbación.
Una onda transporta energía y cantidad de movimiento pero no transporta materia: las partículas vibran alrededor de la posición de equilibrio pero no viajan con la perturbación.
Veamos un ejemplo: la onda que transmite un látigo lleva una energía que se descarga al golpear su punta. Las partículas del látigo vibran, pero no se desplazan con la onda.
Las partículas perturbadas por la onda sufren unas fuerzas variables en dirección e intensidad que les producen una aceleración variable y un M.A.S.
Un impulso único, una vibración única en el extremo de una cuerda, al propagarse por ella origina un tipo de onda llamada pulso. Las partículas oscilan una sola vez al paso del pulso, transmiten la energía y se quedan como estaban inicialmente. El pulso sólo está un tiempo en cada lugar del espacio. El sonido de un disparo es un pulso de onda sonora.
Si las vibraciones que aplicamos al extremo de la cuerda se suceden de forma continuada se forma un tren de ondas que se desplazará a lo largo de la cuerda. Las partículas perturbadas por la onda sufren unas fuerzas variables en dirección e intensidad que les producen una aceleración variable y un M.A.S.
Pulso y tren de ondas
El movimiento de cualquier objeto material en un medio (aire, agua, etc) puede ser considerado como una fuente de ondas. Al moverse perturba el medio que lo rodea y esta perturbación, al propagarse, puede originar un pulso o un tren de ondas.Un impulso único, una vibración única en el extremo de una cuerda, al propagarse por ella origina un tipo de onda llamada pulso. Las partículas oscilan una sola vez al paso del pulso, transmiten la energía y se quedan como estaban inicialmente. El pulso sólo está un tiempo en cada lugar del espacio. El sonido de un disparo es un pulso de onda sonora.
Pulsa aquí y prueba a generar pulsos y ondas
En función del tipo de soporte que requieren para su propagación las ondas se clasifican en mecánicas y electromagnéticas. Las mecánicas requieren un medio elástico para propagarse y las electromagnéticas no, se pueden propagar en el vacío.
Si las partículas del medio en el que se propaga la perturbación vibran perpendicularmente a la dirección de propagación las ondas se llaman transversales. Si vibran en la misma dirección se llaman longitudinales.
Tipos de ondas: ondas transversales y ondas longitudinales
Si las clasificamos en función de como vibran respecto a la dirección de propagación tenemos las ondas transversales y las longitudinales.
Aceptaremos que la forma de los pulsos no varía durante la propagación, lo cual sólo es sólo cierto para las ondas electromagnéticas propagándose en el vacío. Las demás ondas se atenúan.
Vamos a referirnos únicamente a ondas cuyos pulsos pueden ser descritos por las funciones matemáticas seno y coseno. Lamamos a estas ondas ondas armónicas. Las partículas del medio en que se propaga una ondas transversal (en este caso las de la cuerda) vibran perpendicularmente a la posición inicial de la cuerda, separándose de la posición inicial, subiendo y bajando con un movimiento vibratorio armónico simple.
La separación de la posición de equilibrio responde a la fórmula y(t )=A· sen (w t), donde A es la amplitud o separación máxima. La velocidad de vibración de las partículas es variable ( v=A ·w·cos wt ), perpendicular a la dirección de propagación y diferente de la velocidad de propagación del pulso (V) que es constante.
Las ondas tranversales tienen crestas y valles y las longitudinales tienen compresiones y dilataciones. En los dos tipos de ondas una partícula siempre se separa armónicamente de la posición de equilibrio.
Si una onda interfiere con otra en determinados puntos puede ocurrir que se anule la vibración formándose un nodo (mira el dibujo animado del inicio de la página que representa la onda estacionaria en una cuerda).
Las ondas longitudinales (como las del sonido) se propagan en medios con resistencia a la compresión (gases, líquidos y sólidos) y las transversales necesitan medios con resistencia a la flexión, como la superficie de un líquido, y en general medios rígidos. Los gases y los líquidos no transmiten las ondas transversales.
Pulsa aquí para ver la relación entre la longitud de onda y la frecuencia
Las ondas viajeras a lo largo de una cuerda son ondas unidimensionales y, como todas las ondas, realizan una transmisión de energía y cantidad de movimiento sin transporte de materia.
Cuando dos ondas se cruzan se producen los fenómenos de interferencia que afectan a las partículas que están en el cruce pero no a las ondas, de manera que cada una sigue su camino sin alterar ninguna de sus características ni el valor de la energía transportada.
Realiza, observa y comprueba lo anterior en la propagación de una onda en una cuerda tensa.
También puedes observar, pulsando aquí, como son las ondas que dan lugar a las olas del mar
Son aquellas ondas que no necesitan un medio material para propagarse. Incluyen, entre otras, la luz visible y las ondas de radio, televisión y telefonía.
El científico neerlandés Christoph Hendrik Diederik Buys Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y confirmó que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como "efecto Doppler-Fizeau" y en los Países Bajos como el "efecto Doppler-Gestirne".
En el caso del espectro visible de la radiación electromagnética, si el objeto se aleja, su luz se desplaza a longitudes de onda más largas, desplazándose hacia el rojo. Si el objeto se acerca, su luz presenta una longitud de onda más corta, desplazándose hacia el azul. Esta desviación hacia el rojo o el azul es muy leve incluso para velocidades elevadas, como las velocidades relativas entre estrellas o entre galaxias, y el ojo humano no puede captarlo, solamente medirlo indirectamente utilizando instrumentos de precisión como espectrómetros. Si el objeto emisor se moviera a fracciones significativas de la velocidad de la luz, sí sería apreciable de forma directa la variación de longitud de onda.
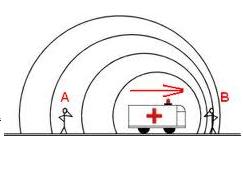
Sin embargo hay ejemplos cotidianos de efecto Doppler en los que la velocidad a la que se mueve el objeto que emite las ondas es comparable a la velocidad de propagación de esas ondas. La velocidad de una ambulancia (50 km/h) puede parecer insignificante respecto a la velocidad del sonido al nivel del mar (unos 1.235 km/h), sin embargo se trata de aproximadamente un 4% de la velocidad del sonido, fracción suficientemente grande como para provocar que se aprecie claramente el cambio del sonido de la sirena desde un tono más agudo a uno más grave, justo en el momento en que el vehículo pasa al lado del observador
Vamos a referirnos únicamente a ondas cuyos pulsos pueden ser descritos por las funciones matemáticas seno y coseno. Lamamos a estas ondas ondas armónicas. Las partículas del medio en que se propaga una ondas transversal (en este caso las de la cuerda) vibran perpendicularmente a la posición inicial de la cuerda, separándose de la posición inicial, subiendo y bajando con un movimiento vibratorio armónico simple.
La separación de la posición de equilibrio responde a la fórmula y(t )=A· sen (w t), donde A es la amplitud o separación máxima. La velocidad de vibración de las partículas es variable ( v=A ·w·cos wt ), perpendicular a la dirección de propagación y diferente de la velocidad de propagación del pulso (V) que es constante.
Las ondas tranversales tienen crestas y valles y las longitudinales tienen compresiones y dilataciones. En los dos tipos de ondas una partícula siempre se separa armónicamente de la posición de equilibrio.
Si una onda interfiere con otra en determinados puntos puede ocurrir que se anule la vibración formándose un nodo (mira el dibujo animado del inicio de la página que representa la onda estacionaria en una cuerda).
Las ondas longitudinales (como las del sonido) se propagan en medios con resistencia a la compresión (gases, líquidos y sólidos) y las transversales necesitan medios con resistencia a la flexión, como la superficie de un líquido, y en general medios rígidos. Los gases y los líquidos no transmiten las ondas transversales.
Longitud de onda, frecuencia y periodo
Se define la longitud de onda, l, como la distancia que recorre el pulso mientras un punto realiza una oscilación completa. El tiempo que tarda en realizar una oscilación se llama periodo ( T ) y la frecuencia ( n ) es el número de oscilaciones (vibraciones) que efectúa cualquier punto de la onda en un segundo. Las ondas viajeras a lo largo de una cuerda son ondas unidimensionales y, como todas las ondas, realizan una transmisión de energía y cantidad de movimiento sin transporte de materia.
Cuando dos ondas se cruzan se producen los fenómenos de interferencia que afectan a las partículas que están en el cruce pero no a las ondas, de manera que cada una sigue su camino sin alterar ninguna de sus características ni el valor de la energía transportada.
Realiza, observa y comprueba lo anterior en la propagación de una onda en una cuerda tensa.
También puedes observar, pulsando aquí, como son las ondas que dan lugar a las olas del mar
ONDAS ELECTROMAGNÉTICAS |
Todas se propagan en el vacío a una velocidad constante, muy alta (300 0000 km/s) pero no infinita. Gracias a ello podemos observar la luz emitida por una estrella lejana hace tanto tiempo que quizás esa estrella haya desaparecido ya. O enterarnos de un suceso que ocurre a miles de kilómetros prácticamente en el instante de producirse.
Las ondas electromagnéticas se propagan mediante una oscilación de campos eléctricos y magnéticos. Los campos electromagnéticos al "excitar" los electrones de nuestra retina, nos comunican con el exterior y permiten que nuestro cerebro "construya" el escenario del mundo en que estamos.
Las O.E.M. son también soporte de las telecomunicaciones y el funcionamiento complejo del mundo actual.
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
Para saber más sobre su origen y propagación pulsa aquí
El efecto Doppler, llamado así por el físico austríaco Christian Andreas Doppler, es el aparente cambio de frecuencia de una onda producida por el movimiento relativo de la fuente respecto a su observador. Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz en estrellas binarias y otros astros).Las O.E.M. son también soporte de las telecomunicaciones y el funcionamiento complejo del mundo actual.
ORIGEN Y FORMACIÓN
Las cargas eléctricas al ser aceleradas originan ondas electromagnéticas
 | El campo E originado por la carga acelerada depende de la distancia a la carga, la aceleración de la carga y del seno del ángulo que forma la dirección de aceleración de la carga y al dirección al punto en que medimos el campo( sen q). Un campo electrico variable engendra un campo magnético variable y este a su vez uno electrico, de esta forma las o. e.m. se propagan en el vacio sin soporte material |
CARACTERÍSTICAS de LA RADIACIÓN E.M.
- Los campos producidos por las cargas en movimiento puden abandonar las fuentes y viajar a través del espacio ( en el vacio) creándose y recreándose mutuamente. Lo explica la tercera y cuarta ley de Maxwell.
- Las radiaciones electromagnéticas se propagan en el vacio a la velocidad de la luz "c". Y justo el valor de la velocidad de la luz se deduce de las ecuaciones de Maxwell, se halla a partir de dos constantes del medio en que se propaga para las ondas electricas y magnética .
- Los campos electricos y magnéticos son perpendiculares entre si ( y perpendiculares a la dirección de propagación) y estan en fase: alcanzan sus valores máximos y mínmos al mismo tiempo y su relación en todo momento está dada por E=c· B
- El campo eléctrico procedente de un dipolo está contenido en el plano formado por el eje del dipolo y la dirección de propagación. El enunciado anterior también se cumple si sustituimos el eje del dipolo por la dirección de movimiento de una carga acelerada
- Las ondas electromagnéticas son todas semejantes ( independientemente de como se formen) y sólo se diferencian e n su longitud de onda y frecuencia. La luz es una onda electromagnética
- Las ondas electromagnéticas transmiten energía incluso en el vacio. Lo que vibra a su paso son los campos eléctricos y magnéticos que crean a propagarse. La vibracion puede ser captada y esa energía absorberse.
- Las intensidad instantánea que posee una onda electromagnética, es decir, la energía que por unidad de tiempo atraviesa la unidad de superficie, colocada perpendicularmente a la direción de propagación es: I=c· eoE2. La intensidad media que se propaga es justo la mitad de la expresión anterior.
- La intensidad de la onda electromagnética al espandirse en el espacio disminuuye con el cuadrado de la distancia y como "I "es proporcional a E2 y por tanto a sen2Q . Por lo tanto existen direcciones preferenciales de propagación
ESPECTRO ELECTROMAGNÉTICO-
Pulsa para ver el espectro de las radiaciones
Instrucciones de manejo del applet
Pulsa el botón izquierdo (o derecho) del ratón y arrastra en horizontal para obtener distintas perspectivas de la propagación (alrededor del eje z). Pulsa y arrastre en vertical para girar alrededor del plano xy.
Realización práctica
Realiza, obseva y comprueba lo siguiente:
1-Supón que le campo eléctrico es el de color verde oscuro y vibra en el plano "yz" y el magnético, el granate , vibra en el plano "xz" . Comprueba que alcanzan el máximo y el mímino al mismo tiempo. Lejos de la fuente los campos viajan en fase
2.-Comprueba girando el enfoque con el que los observas que se propagan perpendicularmente entre si y perpendiculares a la dirección de propagación de la onda. Por lo tanto la Onda E.M. es una onda tranvesrsal
3.- Al ser una onda transversal puede ser polarizada. Para comprobar los efectos del polarizador se visualiza sólo el compo eléctrico ( amarillo) vibrando en el plano formado por el eje z y la bisectriz del yx. El polarizador permite que sólo atraviese la componente de proyección sobre el eje y. Comprueba que la amplitud del rayo polarizado (rojo) es siempre menor en cada instante que la del rayo sin polarizar tal como corresponde a su proyección. Mira desde distintas perspectivas la figura respecto al eje z y plano xy.Onda sonora
Hemos definido el sonido como la sensación producida en el oído por las vibraciones de las partículas que se desplazan en forma de onda sonora a través de un medio elástico que las propaga.
Como el sonido se propaga en forma de ondas, tenemos que saber que características tiene la onda sonora para ver como se comporta.
1.- Es una onda mecánica.
Las ondas mecánicas no pueden desplazarse en el vacío, necesitan hacerlo a través de un medio material (aire, agua, cuerpo sólido). Además dicho medio debe ser elástico y no rígido para permitir la transmisión del sonido. Ya hemos visto cómo se propaga la vibración a través de las partículas o moléculas que conforman el medio, si quieres volver a verlo pulsa aquí.
2.- Es una onda longitudinal.
En las ondas longitudinales el movimiento de las partículas se desplazan en la misma dirección que la onda. Ver animación.
 |  |
Ondas longitudinales
Mientras que en las ondas transversales el movimiento de las partículas es perpendicular a la dirección de la onda. Ver animación.
Si quieres ver otros ejemplos en los que aparecen ambos tipos de ondas, pulsa los siguientes enlaces: enlace 1 - enlace 2 .
En cualquiera de los dos casos, las partículas oscilan alrededor de un punto de reposo, bien horizontalmente o verticalmente pero no se desplazan hacia el final. Es decir lo que se transmite o propaga a través del medio es la energía o vibración, no la materia.
Te preguntarás qué pasa con la vibraciones de las cuerdas. Pues sí, estas son ondas transversales. pero el sonido llega a nosotros a partir de las ondas longitudinales que aquellas generan.
 |  |
En este ejemplo podrás observar también las ondas longitudinales que generan las cuerdas al vibrar transversalmente. Tienes que pulsar el botón "See" , además puedes variar la tensión de la cuerda, aumentando así su frecuencia.
3.- Es una onda tridimensional.
Son ondas que se propagan en tres direcciones. Las ondas tridimensionales se conocen también como ondas esféricas, porque sus frentes de ondas son esferas concéntricas que salen de la fuente de perturbación expandiéndose en todas direcciones.
 |  |
Características de las ondas
Amplitud
Puede decirse que es la altura de la onda. Es la máxima distancia que alcanza un punto al paso de las ondas respecto a su posición de equilibrio. La amplitud está relacionada con la intensidad sonora, a menor amplitud menor intensidad y a mayor amplitud mayor intensidad.
 |  |
Amplitud de una onda longitudinal
Amplitud de una onda
El decibelio es la principal unidad de medida utilizada para el nivel de potencia o nivel de intensidad del sonido. Los sonidos que percibimos deben superar el umbral auditivo (0 dB) y no llegar al umbral de dolor (140 dB). Llamamos umbral de dolor a la intensidad máxima de sonido a partir de la cual el sonido produce en el oído sensación de dolor.
Por encima de los 100 dB es muy recomendable siempre que sea posible, utilizar protectores para los oídos. En puestos de trabajos, se considera necesario el utilizar protectores en ambientes con niveles de 85 dB, siempre y cuando la exposición sea prolongada. Los daños producidos en el oído por exposiciones a ruidos muy fuertes son acumulativos e irreversibles, por lo que se deben de extremar las precauciones. De la exposición prolongada a ruidos se observan trastornos nerviosos, cardiacos y mentales.
Observa y escucha en el siguiente enlace como va disminuyendo la intensidad (dB) y su relación con la amplitud (en los gráficos se representa con trazos de color verde)
Frecuencia
La frecuencia es el número de ciclos (ondas completas que se producen una unidad de tiempo. En el caso del sonido, la unidad de tiempo es el segundo y la frecuencia se mide en hercios (Hz). Así un frecuencia de 1 Herzio es lo mismo que decir que el sonido tiene una vibración por segundo (por cierto, un sonido de esta frecuencia sería imposible de percibir por el oído humano).
Las frecuencias mas bajas se corresponden con lo que habitualmente llamamos sonidos "graves" , son sonidos de vibraciones lentas. Las frecuencias mas altas se corresponden con lo que llamamos sonidos "agudos" y son vibraciones muy rápidas.
 |  |
En este enlace puedes ver el tipo de ondas dependiendo de la frecuencia, para ello tienes escribir en el recuadro perteneciente a frecuencia, el valor que desees y posteriormente dar a "calcular".
Si quieres comprobar cual es tu sensibilidad a los cambios de frecuencia en estos enlaces lo podrás averiguar: enlace 1 - enlace 2.
En este otro enlace puedes variar la frecuencia deslizando el botón correspondiente, obteniendo sonidos agudos si aumentas la frecuencia y sonidos graves si las disminuyes.
El espectro de frecuencias audible varia según cada persona, edad etc. Sin embrago normalmente se acepta como el intervalo entre 20 Hz y 20.000 Hz. Por debajo de esta medida se encontrarían los infrasonidos que son vibraciones de presión, cuya frecuencia es inferior a la que el oído humano puede percibir, es decir, entre 0 y 20 Hz. Por encima estarían los ultrasonidos, que son aquellas ondas cuya frecuencia es superior al margen de audición humana, es decir superior a los 20.000 Hz.
Busca que aplicaciones pueden tener estos dos tipos de sonidos, los infrasonidos y los ultrasonidos, para ello acude a estos enlaces : enlace 1 - enlace 2.
La longitud de onda
Indica el tamaño de una onda, que es la distancia entre el principio y el final de una onda completa (ciclo).
la longitud de onda y la frecuencia de una onda están relacionadas, son inversamente proporcionales: A mayor frecuencia menor longitud de onda y viceversa.
Puedes comprobarlo en el siguiente enlace, deslizando con el ratón hacia la izquierda o hacia la derecha, cambiando así los valores de la longitud (color azul) o el de la frecuencia (color verde), verás como aumentando el valor de una disminuye el de la otra.
Forma de onda
La forma de onda es la característica que nos permitirá distinguir una nota de la misma frecuencia e intensidad producida por instrumentos diferentes. La forma de onda viene determinada por los armónicos.
Normalmente, al hacer vibrar un cuerpo, no obtenemos un sonido puro, sino un sonido compuesto de sonidos de diferentes frecuencias. A estos se les llama armónicos Los armónicos contribuyen a la percepción auditiva de la calidad de sonido o timbre
Cuando se ejecuta una nota en un instrumento musical se genera una onda de presión de aire. Esta onda sonora está acompañada por una serie de armónicos, todos prácticamente inaudibles, pero que le dan al instrumento su timbre particular.
 |  |
En este enlace podrás ver representados en colores, los armónicos de la cuerda de un violín.
El científico neerlandés Christoph Hendrik Diederik Buys Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y confirmó que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como "efecto Doppler-Fizeau" y en los Países Bajos como el "efecto Doppler-Gestirne".
En el caso del espectro visible de la radiación electromagnética, si el objeto se aleja, su luz se desplaza a longitudes de onda más largas, desplazándose hacia el rojo. Si el objeto se acerca, su luz presenta una longitud de onda más corta, desplazándose hacia el azul. Esta desviación hacia el rojo o el azul es muy leve incluso para velocidades elevadas, como las velocidades relativas entre estrellas o entre galaxias, y el ojo humano no puede captarlo, solamente medirlo indirectamente utilizando instrumentos de precisión como espectrómetros. Si el objeto emisor se moviera a fracciones significativas de la velocidad de la luz, sí sería apreciable de forma directa la variación de longitud de onda.
Sin embargo hay ejemplos cotidianos de efecto Doppler en los que la velocidad a la que se mueve el objeto que emite las ondas es comparable a la velocidad de propagación de esas ondas. La velocidad de una ambulancia (50 km/h) puede parecer insignificante respecto a la velocidad del sonido al nivel del mar (unos 1.235 km/h), sin embargo se trata de aproximadamente un 4% de la velocidad del sonido, fracción suficientemente grande como para provocar que se aprecie claramente el cambio del sonido de la sirena desde un tono más agudo a uno más grave, justo en el momento en que el vehículo pasa al lado del observador
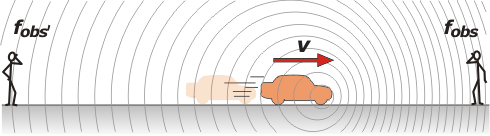
¿ Has notado cómo el tono de las sirenas de las ambulancias, de los bomberos o de la policía, cambia a medida que el auto se nos acerca?. La frecuencia es mayor a medida que el auto se nos acerca, luego, cambia súbitamente a una frecuencia menor a medida que se aleja. Este fenómeno es conocido como el Efecto Doppler. (La frecuencia es el número de vibraciones completas por segundo medidas en una posición fija).
En este dibujo se puede ilustrar este efecto. La fuente sonora se mueve hacia la derecha, con una cierta velocidad, emitiendo ondas que se propagan en círculos centrados en la posición de la fuente (los observadores están ubicados uno adelante y otro atrás de la fuente en el momento que se generan las ondas.)
La frecuencia de la fuente sonora no cambia, pero cuando la fuente se acerca hacia el observador de adelante, más ondas se acumulan entre ellos. La longitud de onda se acorta. Aunque la velocidad del sonido no cambia, la frecuencia del sonido detectado aumenta.
En cambio, cuando la fuente se aleja del detector (de la persona que está detrás), la longitud de onda aumenta y la frecuencia detectada es menor. El efecto Doppler también se presenta si la fuente se encuentra estacionaria, y el detector está en movimiento.
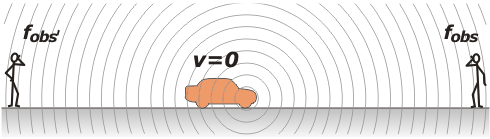
Si la fuente emisora está detenida (sin movimiento) ambos observadores percibirán la misma frecuencia en la misma longitud de onda.
Si la fuente emisora se mueve hacia adelante las ondas se juntan (se acortan) aumentando la frecuencia. Para el observador de atrás, las ondas se alargan (se separan), disminuyendo la frecuencia.
Aplicaciones del Efecto Doppler
El efecto Doppler posee muchas aplicaciones. Los detectores de radar lo utilizan para medir la rapidez de los automóviles y de las pelotas en varios deportes.
Los astrónomos utilizan el efecto Doppler de la luz de galaxias distantes para medir su velocidad y deducir su distancia.
Los médicos usan fuentes de ultrasonido para detectar las palpitaciones del corazón de un feto; los murciélagos lo emplean para detectar y cazar a un insecto en pleno vuelo. Cuando el insecto se mueve más rápidamente que el murciélago, la frecuencia reflejada es menor, pero si el murciélago se está acercando al insecto, la frecuencia reflejada es mayor.
Para ver una animación del Efecto Doppler, ir a:
Colocar el cursor en un punto cualquiera de la pantalla y hacer clic: el efecto Doppler se desplegarlas para saber cómo percibe el sonido alguien ubicado en este
punto
Espejos esféricos
Elementos de um espejo esférico
Los espejos esféricos tienen la forma de la superficie que resulta cuando una esfera es cortada por un plano. Si la superficie reflectora está situada en la cara interior de la esfera se dice que el espejo es cóncavo. Si está situada en la cara exterior se denomina convexo. Las características ópticas fundamentales de todo espejo esférico son las siguientes:
su formula es n=360/<a-1. Donde n=numero de imagenes, 360=< perigonal, <a=angulo de abertura, -1=el objeto reflejado.
Asimismo, cuando un rayo incide paralelamente al eje, el rayo reflejado pasa por el foco, y, viceversa, si el rayo incidente pasa por el foco el reflejado marcha paralelamente al eje. Es ésta una propiedad fundamental de los rayos luminosos que se conoce como reversibilidad.
Con estas reglas, que son consecuencia inmediata de las leyes de la reflexión, es posible construir la imagen de un objeto situado sobre el eje principal cualquiera que sea su posición. Basta trazar dos rayos incidentes que, emergiendo del extremo superior del objeto discurran uno paralelamente al eje y el otro pasando por el centro de curvatura C; el extremo superior del objeto vendrá determinado por el punto en el que ambos rayos convergen. Cuando la imagen se forma de la convergencia de los rayos y no de sus prolongaciones se dice que la imagen es real.
En la construcción de imágenes en espejos cóncavos y según sea la posición del objeto, se pueden plantear tres situaciones diferentes que pueden ser analizadas mediante diagramas de rayos:
a) El objeto está situado respecto del eje más allá del centro de curvatura C. En tal caso la imagen formada es real, invertida y de menor tamaño que el objeto.
b) El objeto está situado entre el centro de curvatura C y el foco F. La imagen resulta entonces real, invertida y de mayor tamaño que el objeto.
c) El objeto está situado entre el foco F y el vértice V. El resultado es una imagen virtual, directa y de mayor tamaño que el objeto.
Para espejos convexos sucede que cualquiera que fuere la distancia del objeto al vértice del espejo la imagen es virtual, directa y de menor tamaño. Dicho resultado puede comprobarse efectuando la construcción de imágenes mediante diagramas de rayos de acuerdo con los criterios anteriormente expuestos.
su formula es n=360/<a-1. Donde n=numero de imagenes, 360=< perigonal, <a=angulo de abertura, -1=el objeto reflejado
Los espejos son quizá el instrumento óptico más antiguo. Los egipcios de hace cuatro mil años emplearon metales pulidos para reflejar sus caras. Sin embargo, no fue sino hasta 1857 cuando se inventaron los espejos gracias a Jean Foucault, quien desarrolló un método para recubrir el vidrio con una capa de plata.
Si una persona se mira en un espejo, como por ejemplo en el espejo del baño, apreciará su imagen en un espejo plano. Un espejo plano es una superficie plana y lisa que refleja la luz de manera regular. En el ejemplo, la persona que se mira es el objeto. Un objeto es una fuente de rayos divergentes de luz que puede ser luminoso como una vela o una lámpara o iluminado como la Luna o la página de un libro que esté leyendo. En el caso de un objeto iluminado, éste refleja la luz de manera difusa en todas direcciones.
La figura a la derecha muestra cómo algunos de los rayos inciden desde el punto P sobre el espejo y se reflejan con ángulos de incidencia y reflexión iguales (recordar que el ángulo de incidencia se forma cuando llega el rayo a la superficie y el de reflexión cuando se devuelve).
Luego de la reflexión, los rayos continúan dispersándose. Si se prolongan los rayos hacia atrás (líneas de visión), por la parte posterior del espejo, como se ve con las líneas discontinuas, se puede observar en el dibujo que se intersecan en el punto P'. El punto P', en donde los rayos prolongados aparentemente se intersecan, se llama imagen. Aun cuando para un observador, los rayos parecen venir del punto P', se observa que allí no existe fuente alguna. Por tal razón, esta imagen se denomina imagen virtual.
Si se examina la superficie interna de una cuchara se tiene un espejo cóncavo, el cual refleja la luz. Está conformado por un número muy grande de espejos planos pequeños montados sobre la superficie de una esfera.
Un espejo convexo es un objeto esférico que refleja luz desde la superficie externa. La parte externa de una cuchara es un ejemplo. Los rayos reflejados siempre divergen y, por tanto, no forman imágenes reales
punto
Espejos esféricos
De Wikilibros, la colección de libros de texto de contenido libre.
Física/Óptica/Espejos esféricos
su formula es n=360/<a-1. Donde n=numero de imagenes, 360=< perigonal, <a=angulo de abertura, -1=el objeto reflejado.
- Centro de curvatura C: Es el centro de la superficie esférica que constituye el espejo.
- Radio de curvatura R: Es el radio de dicha superficie.
- Vértice V: Coincide con el centro del espejo.
- Eje principal: Es la recta que une el centro de curvatura C con el vértice V.
- Foco: Es un punto del eje por el que pasan o donde convergen todos los rayos reflejados que inciden paralelamente al eje. En los espejos esféricos se encuentra en el punto medio entre el centro de curvatura y el vértice.
Formación de imágenes en espejos esféricos[editar]
Cuando un rayo incidente pasa por el centro de curvatura, el rayo reflejado recorre el mismo camino, pero en sentido inverso debido a que la incidencia es normal o perpendicular.Asimismo, cuando un rayo incide paralelamente al eje, el rayo reflejado pasa por el foco, y, viceversa, si el rayo incidente pasa por el foco el reflejado marcha paralelamente al eje. Es ésta una propiedad fundamental de los rayos luminosos que se conoce como reversibilidad.
Con estas reglas, que son consecuencia inmediata de las leyes de la reflexión, es posible construir la imagen de un objeto situado sobre el eje principal cualquiera que sea su posición. Basta trazar dos rayos incidentes que, emergiendo del extremo superior del objeto discurran uno paralelamente al eje y el otro pasando por el centro de curvatura C; el extremo superior del objeto vendrá determinado por el punto en el que ambos rayos convergen. Cuando la imagen se forma de la convergencia de los rayos y no de sus prolongaciones se dice que la imagen es real.
En la construcción de imágenes en espejos cóncavos y según sea la posición del objeto, se pueden plantear tres situaciones diferentes que pueden ser analizadas mediante diagramas de rayos:
a) El objeto está situado respecto del eje más allá del centro de curvatura C. En tal caso la imagen formada es real, invertida y de menor tamaño que el objeto.
b) El objeto está situado entre el centro de curvatura C y el foco F. La imagen resulta entonces real, invertida y de mayor tamaño que el objeto.
c) El objeto está situado entre el foco F y el vértice V. El resultado es una imagen virtual, directa y de mayor tamaño que el objeto.
Para espejos convexos sucede que cualquiera que fuere la distancia del objeto al vértice del espejo la imagen es virtual, directa y de menor tamaño. Dicho resultado puede comprobarse efectuando la construcción de imágenes mediante diagramas de rayos de acuerdo con los criterios anteriormente expuestos.
su formula es n=360/<a-1. Donde n=numero de imagenes, 360=< perigonal, <a=angulo de abertura, -1=el objeto reflejado
Los espejos son quizá el instrumento óptico más antiguo. Los egipcios de hace cuatro mil años emplearon metales pulidos para reflejar sus caras. Sin embargo, no fue sino hasta 1857 cuando se inventaron los espejos gracias a Jean Foucault, quien desarrolló un método para recubrir el vidrio con una capa de plata.
| a) Espejos planos |
 |
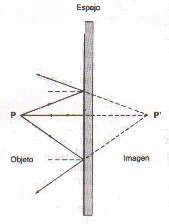La figura a la derecha muestra cómo algunos de los rayos inciden desde el punto P sobre el espejo y se reflejan con ángulos de incidencia y reflexión iguales (recordar que el ángulo de incidencia se forma cuando llega el rayo a la superficie y el de reflexión cuando se devuelve).
Luego de la reflexión, los rayos continúan dispersándose. Si se prolongan los rayos hacia atrás (líneas de visión), por la parte posterior del espejo, como se ve con las líneas discontinuas, se puede observar en el dibujo que se intersecan en el punto P'. El punto P', en donde los rayos prolongados aparentemente se intersecan, se llama imagen. Aun cuando para un observador, los rayos parecen venir del punto P', se observa que allí no existe fuente alguna. Por tal razón, esta imagen se denomina imagen virtual.
| b) Espejo cóncavo |
 |
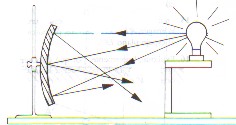Si se examina la superficie interna de una cuchara se tiene un espejo cóncavo, el cual refleja la luz. Está conformado por un número muy grande de espejos planos pequeños montados sobre la superficie de una esfera.
| c) Espejo convexo |
 |
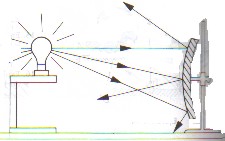Un espejo convexo es un objeto esférico que refleja luz desde la superficie externa. La parte externa de una cuchara es un ejemplo. Los rayos reflejados siempre divergen y, por tanto, no forman imágenes reales
No hay comentarios.:
Publicar un comentario